Lógica Difusa: Introducción, Conjuntos Certeros vs Difusos
Lógica Clásica vs Lógica Difusa
Lógica Clásica
Verdadero => 1
False => 0
verdacidad \in \{ 0 , 1 \}Indica si un elemento pertenece o no a un conjunto, si se tienen dos grupos disyuntivos el elemento pertenece a uno u otro.
Lógica Difusa
Parcialmente Verdadero => 0.65
Parcialmente Falso => 0.35
veracidad \in [ 0.0, 1.0 ]
Indica el “grado” en que un elemento pertenece a un grupo, si se tienen dos grupos disyuntivos un elemento puede pertenecer a ambos, pero en diferente grado.
Universo de Discurso -> La totalidad
X \in [a,b] ; a,b \in R
Función de Membresía
\mu(x) \to [0, 1]
Dominio => Universo de Discurso
x \in X
Imagen =>
\mu \in [0,1]
Notación de Conjuntos Difusos
Conjuntos Difusos Continuos
Conjuntos Difusos Discretos
A = \left\{ \int \frac{\mu(x)}{x} \right\}A = \left\{ \int\limits_0^{10} \frac{ \exp \left[ - \frac{1}{2} \left( \frac{x-5}{3} \right)^2 \right] }{x} \right\}A = \sum \frac{\mu(x)}{x}A = \left\{ \frac{0}{1} + \frac{0.1}{2} + \frac{0.4}{3} + \frac{0.8}{4} + \frac{1}{5} + \frac{1}{6} + \frac{0.8}{7} + \frac{0.4}{8} + \frac{0.1}{9} + \frac{0}{10} \right\}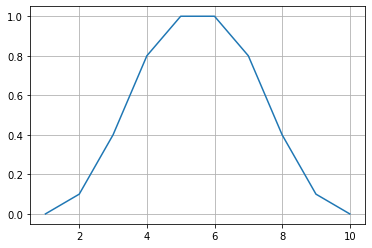
Cardinalidad escalar
|A| = \sum_{x \in X} \mu(x)Operaciones sobre Conjuntos Difusos
Conjuntos Clásicos / Conjuntos Certeros
Conjuntos Difusos
Subconjuntos
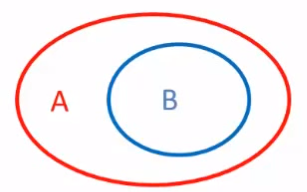
B \subseteq A; \forall b, b \in B \land b \in A
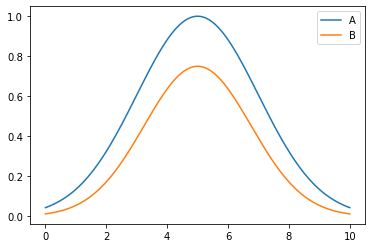
B \subseteq A \leftrightarrow \mu_B(x) \leq \mu_A(x); \forall x \in X
Interseccion
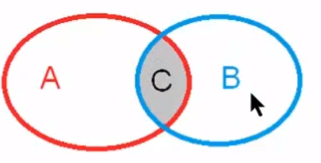
C = A \cap B
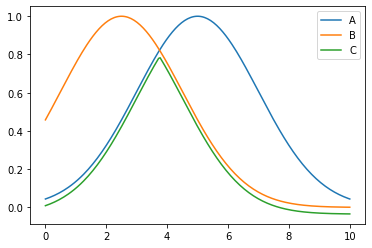
\begin{aligned}
C = A \cap B \leftrightarrow \mu_C(x) & = \min (\mu_A(x), \mu_B(x)) \\
& = \mu_A(x) \land \mu_B(x) \forall x \in X
\end{aligned}Unión
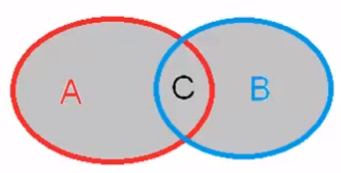
C = A \cup B
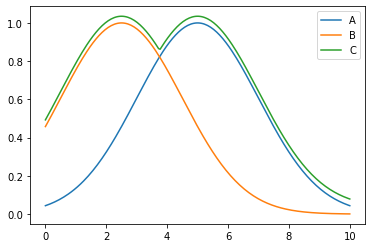
\begin{aligned}
C = A \cup B \leftrightarrow \mu_C(x) & = \max (\mu_A(x), \mu_B(x)) \\
& = \mu_A(x) \lor \mu_B(x) \forall x \in X
\end{aligned}Complemento
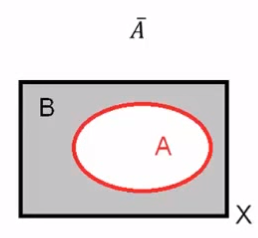
\overline{A}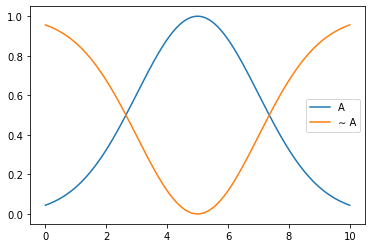
\overline{A} \leftrightarrow \mu_{\sim A} = 1 - \mu_A(x) \forall x \in XPropiedades de las Operaciones Difusas
Conjuntos Clásicos / Conjuntos Certeros
Conjuntos Difusos
Union
Conmutativa
A \cup B = B \cup A
\max( \mu_A, \mu_B ) = \max( \mu_B, \mu_A )
Asociativa
A \cup ( B \cup C ) = ( A \cup B ) \cup C
\begin{aligned}
\max( \mu_A, \max ( \mu_B , \mu_C ) ) &= \max( \mu_A, \mu_B , \mu_C ) \\
& = \max( \max ( \mu_A, \mu_B ) , \mu_C )
\end{aligned}Distributiva
A \cup ( B \cap C ) = ( A \cup B ) \cap ( A \cup C )
\max( \mu_A, \min ( \mu_B , \mu_C ) ) = \min ( \max ( \mu_A, \mu_B ) , \max (\mu_A , \mu_C ) )
Identidad
A \cup \empty = A \\ A \cup X = X
\max ( \mu_A, 0 ) = \mu_A \\ \max ( \mu_A, 1 ) = 1 \\
Idempotencia
A \cup A = A
\max ( \mu_A , \mu_A ) = \mu_A
Complemento
A \cup \overline{A} = X\max( \mu_A, 1 - \mu_A ) \neq 1
Leyes de Morgan
\overline{A \cup B} = \overline{B} \cap \overline{A}1 - \max ( \mu_A, \mu_B ) = \min ( 1 - \mu_A, 1 - \mu_B )
Intersección
Conmutativa
A \cap B = B \cap A
\min( \mu_A, \mu_B ) = \min( \mu_B, \mu_A )
Asociativa
A \cap ( B \cap C ) = ( A \cap B ) \cap C
\begin{aligned}
\min( \mu_A, \min ( \mu_B , \mu_C ) ) &= \min( \mu_A, \mu_B , \mu_C ) \\
& = \min( \min ( \mu_A, \mu_B ) , \mu_C )
\end{aligned}Distributiva
A \cap ( B \cup C ) = ( A \cap B ) \cup ( A \cap C )
\min( \mu_A, \max ( \mu_B , \mu_C ) ) = \max ( \min ( \mu_A, \mu_B ) , \min (\mu_A , \mu_C ) )
Identidad
A \cap \empty = \empty \\ A \cap X = A
\min ( \mu_A, 0 ) = 0 \\ \min ( \mu_A, 1 ) = \mu_A \\
Idempotencia
A \cap A = A
\min ( \mu_A , \mu_A ) = \mu_A
Complemento
A \cap \overline{A} = \empty\min( \mu_A, 1 - \mu_A ) \neq 0
Leyes de Morgan
\overline{A \cap B} = \overline{B} \cup \overline{A}1 - \min ( \mu_A, \mu_B ) = \max ( 1 - \mu_A, 1 - \mu_B )
Otras Propiedades de las Operaciones Difusas
Transitiva
A \subseteq B \land B \subseteq C \rightarrow A \subseteq C
\mu_A \leq \mu_B \land \mu_B \leq \mu_C \rightarrow \mu_A \leq \mu_C
Involutiva
\overline{ \overline{ A } } = A\mu_{\overline{\overline{A}}} = 1 - \mu_{\overline{A}} = 1 - ( 1 - \mu_A ) = \mu_AKlir, G. J., & Yuan, B. (1995). Fuzzy Sets and Fuzzy Logic: Theory and Applications. Prentice Hall.
[Hackeando Tec]. (2015, Agosto 4). Lógica Difusa – Introducción al Curso y Aplicaciones – Hackeando Tec [Video]. YouTube. https://youtu.be/xLFNUo0mTZE?si=xThDAGBM6UudQxPU
[Hackeando Tec]. (2015, Agosto 14). Lógica Difusa – 1.0 Conjuntos Difusos (Contenido) – Hackeando Tec [Video]. YouTube. https://youtu.be/l3JmHL3dNHc?si=Xz9QnQwh-vP0sYGw
[Hackeando Tec]. (2015, Agosto 14). Lógica Difusa – 1.1 Conjuntos Certeros vs Difusos – Hackeando Tec [Video]. YouTube. https://youtu.be/4EkDfPK09Ng?si=YGJ-r5bnw3daKDdU
[Hackeando Tec]. (2015, Agosto 14). Lógica Difusa – 1.2 Operaciones entre Conjuntos Difusos – Hackeando Tec [Video]. YouTube. https://youtu.be/DFyLBEMnJdE?si=8_3QwZrRLHicqKzQ
[Hackeando Tec]. (2015, Agosto 21). Lógica Difusa – 1.3 Propiedades de las operaciones difusas – Parte 1 – Hackeando Tec [Video]. YouTube. https://youtu.be/gLQWaaYHD_0?si=mIxvCnTAqtViapDf
[Hackeando Tec]. (2015, Agosto 21). Lógica Difusa – 1.3 Propiedades de las operaciones difusas – Parte 2 – Hackeando Tec [Video]. YouTube. https://youtu.be/Le3Nf5K0VwE?si=yCYyx-K5bZFZ9AC6
