Lógica Difusa: Operadores Difusos Generalizados
Norma T – Norma Triangular
La intersección de A y B puede representarse en general como:
T:[0,1] \times [0,1] \to [0,1]
o bien como un operador binario:
\mu_{A \cap B} (x,y) = T( \mu_A (x), \mu_B (y) ) = \mu_A (x) \bigtriangleup \mu_B (y)La norma T debe cumplir las siguientes propiedades:
- Acotada
T(0,0) = 0 \land T(a,1) = T(1,a)=a
- Monotónica
a \leq c \land b \leq d \to T(a,b) \leq T(c,d)
- Conmutativa
T(a,b) = T(b,a)
- Asociativa
T(a, T(b,c)) = T(T(a,b),c)
Ejemplos
Mínimo:
T_{min}(a,b) = \min(a,b) = a \land bProducto Frontera:
T_{bp} = \max ( 0 , a + b - 1 ) = 0 \lor (a + b -1)Producto Algebraico:
T_{ab} (a,b) = a bProducto Drástico
T_{dp} = \left\{ \begin{matrix}
a, & si & b = 1 \\
b, & si & a = 1 \\
0, & si & a, b < 1 \\
\end{matrix} \right.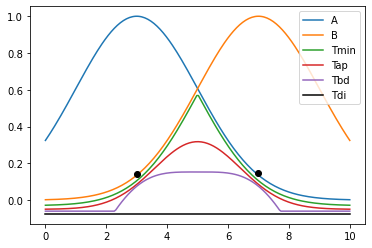
Norma S – Norma Co-triangular
La intersección de A y B puede representarse en general como:
S : [0,1] \times [0,1] \to [0,1]
o bien como un operador binario:
\mu_{A \cup B} (x,y) = S( \mu_A(x), \mu_B(y) ) = \mu_A(x) \perp \mu_B(y)La norma S debe cumplir las siguientes propiedades:
- Acotada
S(1,1) = 1 \land T(a,0) = T(0,a) = a
- Monotónica
a \leq c \land b \leq d \to S(a,b) \leq S(c,d)
- Conmutativa
S(a,b) = S(b,a)
- Asociativa
S(a, S(b,c)) = S(S(a,b),c)
Ejemplos
Máximo:
S_{max} = \max(a,b) = a \lor bSuma Frontera:
S_{bs} (a,b) = \min (1, a + b ) = 1 \land (a+b)Suma Algebraica:
S_{as} (a,b) = a + b - a bSuma Drástica:
T_{dp} = \left\{ \begin{matrix}
a, & si & b = 0 \\
b, & si & a = 0 \\
1, & si & a, b > 0 \\
\end{matrix} \right.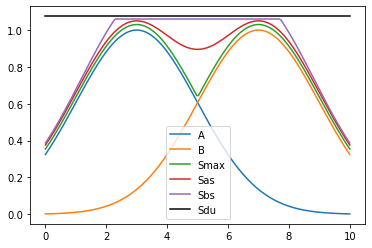
Complemento Difuso
El complemento difuso de un conjunto difuso A puede generalizarse considerándolo como una función N:
N:[0,1] \to [0,1] \text{ tal que } \mu_{ \neg A}(x) = N( \mu_{A} (x) )El complemento difuso debe cumplir las siguientes propiedades:
- Acotada
N(0) = 1 \land N(1) = 0
- Monotónica
a \leq b \land \to N(a) \geq N(b)
- Involutiva
N(N(a)) = a
Ejemplos:
Complemento clásico:
N_c(a) = 1 - a
Complemento de Yager:
N_w(a) = (1 - a^w)^{\frac{1}{w}} \\
\text{donde } w > 0Complemento de Sugeno:
N_s(a) = \frac{1-a}{1+sa} \\
\text{donde } s > -1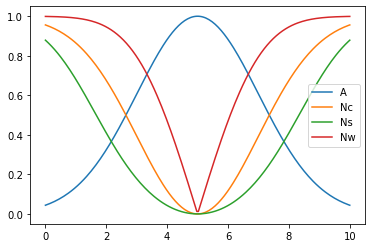
[Hackeando Tec]. (2015, Agosto 23). Lógica Difusa – 2.2.1 Operadores Difusos Generalizados (Normas T) – Hackeando Tec [Video]. YouTube. https://youtu.be/VbWH1QO9VLU?si=BMd-YjaAfB_bLXRV
[Hackeando Tec]. (2015, Agosto 23). Lógica Difusa – 2.2.2 Operadores Difusos Generalizados (Normas S) – Hackeando Tec [Video]. YouTube. https://youtu.be/dgVnKBYX0FA?si=tioByhYM7nBEdajq
[Hackeando Tec]. (2015, Agosto 23). Lógica Difusa – 2.2.3 Operadores Difusos Generalizados (Complemento Difuso) – Hackeando Tec [Video]. YouTube. https://youtu.be/SM9gY325Gm4?si=OJ-RASRsJEjuYnAB
