Lógica Difusa: Razonamiento Difuso
Lógica clásica:
Una proposición clásica es aquella que puede ser verdadera (1) o falsa (0)
\begin{matrix}
& & \text{Conj.} & \text{Disy.} & \text{Neg.} & \text{Impl.} & \text{Equiv.} & \text{O - excl.} & \text{O - excl. neg.} \\
& & \text{Y} & \text{O} & \text{No} & \text{Si - entonces} & \text{Si y solo si} \\
& & \land & \lor & \neg & \to & \leftrightarrow \\
p & q & p \land q & p \lor q & \neg p & p\to q & p \leftrightarrow q & p \underline{\lor} q & \overline{p \underline{\lor} q} \\
0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 1 \\
0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 \\
1 & 0 & 0 & 1 & 1 & 0 & 0 & 1 & 0 \\
1 & 1 & 1 & 1 & 1 & 1 & 1 & 0 & 1 \\
\end{matrix}\begin{aligned}
p \to q & = \neg p \lor q \\
p \leftrightarrow q & = (p \land q) \lor (\neg p \land \neg q) \\
& = \overline{ p \underline{\lor} q }
\end{aligned}Lógica Difusa
Una proposición clásica es aquella que toma valores de veracidad entre 0 y 1
\begin{aligned}
\text{Conjunción } V( p \land q ) & = \min ( V(p), V(q) ) \\
\text{Disyunción } V( p \lor q ) & = \max ( V(p), V(q) ) \\
\text{Negación } V( p ) & = 1 - V(p) \\
\text{Implicación } V( p\to q ) & = V ( \overline{p} \lor q ) \\
& = \max ( 1 - V(p), V(q) ) \\
\text{Equivalencia } V( p \leftrightarrow q ) & = V [ (p \land q) \lor (\neg p \land \neg q) ] \\
& = \max \{ \min [ V(p), V(q) ], \min [ 1 - V(p), 1- V(q) ] \} \\
\end{aligned}Razonamiento Aproximado
Variable Lingüística
\begin{aligned}
\text{Variable Lingüística} & = ( x, X, T(x), G, M ) \\
x & \text{ nombre} \\
X & \text{ universo de discurso} \\
T(x) & \text{ valores lingüísticos que acepta la variable} \\
G & \text{ regla sintáctica que genera los valores lingüísticos} \\
M & \text{ regla semántica que asocia cada término lingüístico con su significado} \\
\end{aligned}… en un partido de fútbol
\begin{aligned}
x & = \text{ posesión del balón} \\
X & = [0, 90] \text{ minutos} \\
T(x) & = \{ \text{ casi nada, poca, } \\
& \text{ equilibrada, grande, enorme} \} \\
M(\text{casi nada}) & = Sigmoidal(x; -0.3, 20) \\
M(\text{poca}) & = Gausiana(x; 9, 25) \\
M(\text{equilibrada}) & = Gausiana(x; 9, 45) \\
M(\text{grande}) & = Gausiana(x; 9, 65) \\
M(\text{enorme}) & = Sigmoidal(x; 0.3, 70)
\end{aligned}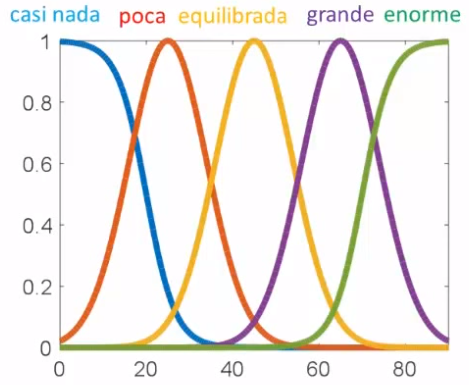
Regla Difusa SI – ENTONCES
si x es A, entonces y es B
x y y son variables lingüísticas
A y B son valores lingüísticos
- Si la presión es alta, entonces el volumen es grande.
- Si la carretera es sinuosa, entonces la carretera es peligrosa.
- Si el jitomate está rojo, entonces el jitomate está maduro.
Interpretación Matemática:
- Relación Difusa R = A × B (mide la intensidad de la relación entre el antecedente y el consecuente). Se emplea en control difuso.
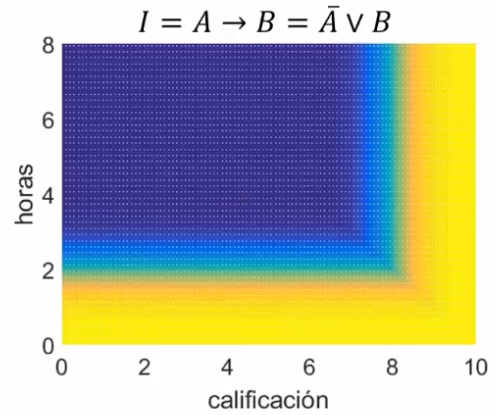
- Implicación Difusa I = A → B (mide la veracidad de la relación entre el antecedente y el consecuente). Se emplea en sistemas expertos, que concluyen o evalúan la veracidad de una sentencia.
… “si estudio mucho, entonces soy un excelente estudiante”
\begin{aligned}
\text{Estudio Mucho } & \to \mu_A = Sigm(x; 0.5, 2) & x \in [0, 8] & \text{ hrs. diarias de estudio} \\
\text{Excelente Estudiante} & \to \mu_B = Sigm(y; 0.5, 8) & y \in [0, 10] & \text{ prom. académico}
\end{aligned}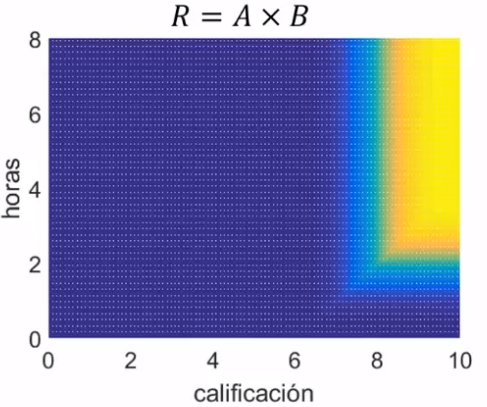
[Hackeando Tec]. (2015, Agosto 28). Lógica Difusa – 3.1 Lógica Clásica vs Difusa – Hackeando Tec [Video]. YouTube. https://youtu.be/nUkqWNxMWeU?si=2SdB4ibwkaEyWu1d
[Hackeando Tec]. (2015, Agosto 28). Lógica Difusa – 3.2.1 Razonamiento Difuso (Variable Lingüística) – Hackeando Tec [Video]. YouTube. https://youtu.be/hjsDioVoIG4?si=n7MT2nWdF7T__AhU
[Hackeando Tec]. (2015, Agosto 28). Lógica Difusa – 3.2.2 Razonamiento Difuso (Regla Si-Entonces) – Hackeando Tec [Video]. YouTube. https://youtu.be/46u5gqd0QDI?si=gzuAU-gcxbTb0B8r
[Hackeando Tec]. (2015, Agosto 28). Lógica Difusa – – Hackeando Tec [Video]. YouTube.
