Lógica Difusa: Funciones de Membresía
Características
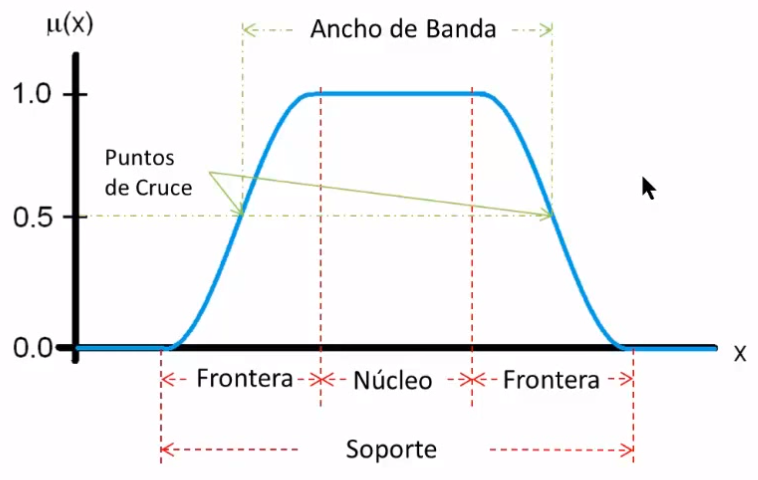
\begin{aligned}
nucleo(A) & = \{ x | \mu_A(x) = 1 \} & & = ^{1}A \\
fronteras(A) & = \{ x | 0 < \mu_A(x) < 1 \} \\
soporte(A) & = \{ x | \mu_A(x) > 0 \} & & = ^{0+}A & & = S(A) = \text{supp}(A) \\
cruce(A) & = \{ x | \mu_A(x) = 0.5 \} \\
ancho(A) & = | x_2 - x_1 | \\
altura(A) & = \sup_{x \ in X} \mu_A(x) & & & & = h(A)
\end{aligned}Tipos de Funciones de Membresía
Normal vs Subnormal
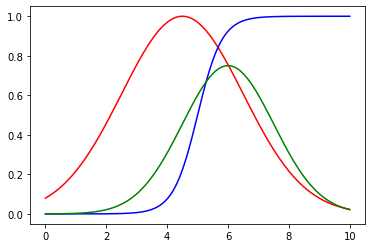
La función de membresía roja y azul son normales (h(A) = 1), ya que llegan a 1, mientras que la verde es subnormal.
Con Núcleo vs Sin Núcleo
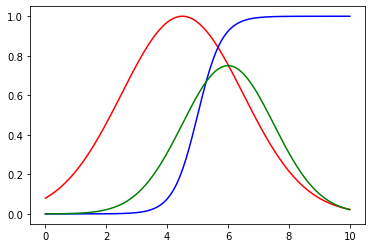
La función de membresía roja y azul son con núcleo, mientras que la verde es sin núcleo.
Convexas vs No Convexas
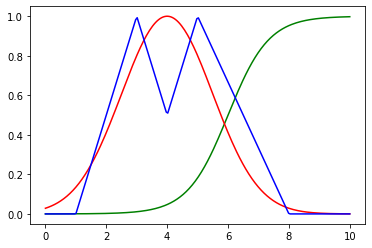
La función de membresía roja y verde son con convexas, mientras que la azul no es convexa.
Criterio de convexion:
\begin{aligned}
\mu_A( x_1 \lambda + (1-\lambda) x_2 ) & \geq \min( \mu_A(x_1), \mu_A(x_2) ) \\
& \forall x_1, x_2 \in X, \\
& \forall \lambda \in [0, 1]
\end{aligned}Simétrica vs No Simétrica
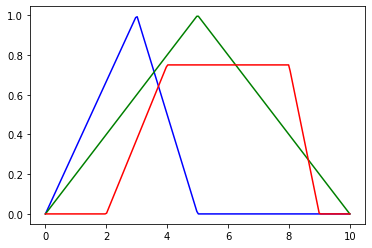
La función de membresía roja y azul no son simétricas, ya que llegan a 1, mientras que la verde si es simétrica.
Abiertas vs Cerradas
Abiertas por la derecha
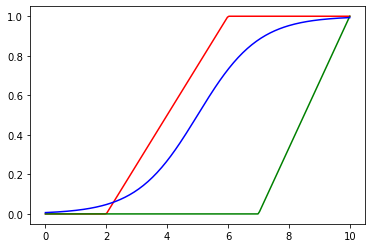
Abiertas por la izquierda
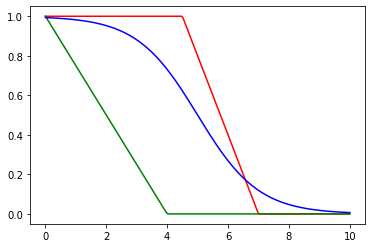
Cerradas
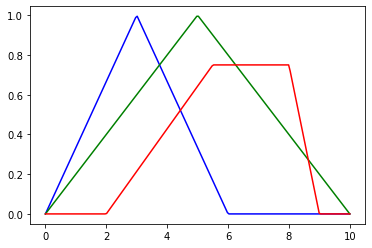
En general las funciones de membresía deberían ser normales y convexas.
Conjunto cortado
\begin{aligned}
\alpha & \in [0, 1] \\
^{\alpha}A = A_{\alpha} & = \{ x | \mu_A(x) \geq \alpha \} \\
^{\alpha +}A = A'_{\alpha} & = \{ x | \mu_A(x) > \alpha \} & \text{
(fuertemente)}
\end{aligned}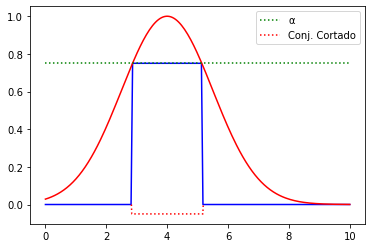
\begin{aligned}
^{\alpha}A & \subseteq {}^{\alpha +}A \\
\alpha \leq \beta & \to {}^{\beta} A \subseteq {}^{\alpha} A \land {}^{\beta +} A \subseteq {}^{\alpha +} A \\
{}^{\alpha} (A \cap B) & = {}^{\alpha} A \cap {}^{\alpha} B \\
{}^{\alpha +} (A \cap B) & = {}^{\alpha +} A \cap {}^{\alpha +} B \\
{}^{\alpha} (A \cup B) & = {}^{\alpha} A \cup {}^{\alpha} B \\
{}^{\alpha +} (A \cup B) & = {}^{\alpha +} A \cup {}^{\alpha +} B \\
{}^{\alpha}(\overline{A}) & = {}^{(1 - \alpha) +} \overline{A}
\end{aligned}\begin{aligned}
\bigcup_{i \in I} {}^{\alpha} A_i & \subseteq {}^{\alpha}\left( \bigcup_{i \in I} A_i \right) \\
\bigcup_{i \in I} {}^{\alpha +} A_i & = {}^{\alpha +}\left( \bigcup_{i \in I} A_i \right) \\
\bigcap_{i \in I} {}^{\alpha} A_i & = {}^{\alpha}\left( \bigcap_{i \in I} A_i \right) \\
\bigcup_{i \in I} {}^{\alpha +} A_i & \subseteq {}^{\alpha +}\left( \bigcap_{i \in I} A_i \right) \\
\end{aligned}\begin{aligned}
A \subseteq B & \leftrightarrow {}^{\alpha} A \subseteq {}^{\alpha} B \\
A \subseteq B & \leftrightarrow {}^{\alpha +} A \subseteq {}^{\alpha +} B \\
A = B & \leftrightarrow {}^{\alpha} A = {}^{\alpha} B \\
A = B &\leftrightarrow {}^{\alpha +} A ={}^{\alpha +} B \\
\end{aligned}{}^{\alpha} A = \bigcap_{\beta < \alpha} {}^{\beta} A = \bigcap_{\beta < \alpha} {}^{\beta +} A \\
{}^{\alpha +} A = \bigcup_{ \alpha < \beta} {}^{\beta} A = \bigcup_{\alpha < \beta} {}^{\beta +} A \\Representación
Considerando el siguiente conjunto difuso:
A = \left\{ \frac{0.2}{x_1} + \frac{0.4}{x_2} + \frac{0.6}{x_3} + \frac{0.8}{x_4} + \frac{1}{x_5} \right\}Puede asociarse a 5 conjuntos cortados definidos por:
{}^{0.2} A = \left\{ \frac{1}{x_1} + \frac{1}{x_2} + \frac{1}{x_3} + \frac{1}{x_4} + \frac{1}{x_5} \right\}, \\
{}^{0.4} A = \left\{ \frac{0}{x_1} + \frac{1}{x_2} + \frac{1}{x_3} + \frac{1}{x_4} + \frac{1}{x_5} \right\}, \\
{}^{0.6} A = \left\{ \frac{0}{x_1} + \frac{0}{x_2} + \frac{1}{x_3} + \frac{1}{x_4} + \frac{1}{x_5} \right\}, \\
{}^{0.8} A = \left\{ \frac{0}{x_1} + \frac{0}{x_2} + \frac{0}{x_3} + \frac{1}{x_4} + \frac{1}{x_5} \right\}, \\
{}^{1} A = \left\{ \frac{0}{x_1} + \frac{0}{x_2} + \frac{0}{x_3} + \frac{0}{x_4} + \frac{1}{x_5} \right\} \\Y convirtiendo cada conjunto cortado de la siguiente forma:
{}_{\alpha} \mu_A(x) = \alpha \cdot {}^{\alpha}\mu_A(x)Obtenemos:
{}_{0.2} A = \left\{ \frac{0.2}{x_1} + \frac{0.2}{x_2} + \frac{0.2}{x_3} + \frac{0.2}{x_4} + \frac{0.2}{x_5} \right\}, \\
{}_{0.4} A = \left\{ \frac{0}{x_1} + \frac{0.4}{x_2} + \frac{0.4}{x_3} + \frac{0.4}{x_4} + \frac{0.4}{x_5} \right\}, \\
{}_{0.6} A = \left\{ \frac{0}{x_1} + \frac{0}{x_2} + \frac{0.6}{x_3} + \frac{0.6}{x_4} + \frac{0.6}{x_5} \right\}, \\
{}_{0.8} A = \left\{ \frac{0}{x_1} + \frac{0}{x_2} + \frac{0}{x_3} + \frac{0.8}{x_4} + \frac{0.8}{x_5} \right\}, \\
{}_{1} A = \left\{ \frac{0}{x_1} + \frac{0}{x_2} + \frac{0}{x_3} + \frac{0}{x_4} + \frac{1}{x_5} \right\} \\
\therefore \\
A = {}_{0.2}A \cup {}_{0.4}A \cup {}_{0.6}A \cup {}_{0.8}A \cup {}_{1}A \\
\uparrow \text{ llamada descomposición de } APrimer teorema de descomposición
A = \bigcup_{\alpha \in [0,1] } {}_\alpha A \\
{}_\alpha A = {}_\alpha \mu_A(x) = \alpha \cdot {}^{\alpha} \mu_A(x)Segundo teorema de descomposición
A = \bigcup_{\alpha \in [0,1] } {}_{\alpha +} A \\
{}_{\alpha +} A = {}_{\alpha +} \mu_A(x) = \alpha \cdot {}^{\alpha +} \mu_A(x)Formas Especiales de las Funciones de Membresía
Singleton
\mu_A = \left \{
\begin{matrix}
1 & x = x_0 \\
0 & x \neq x_0 \\
\end{matrix}
\right.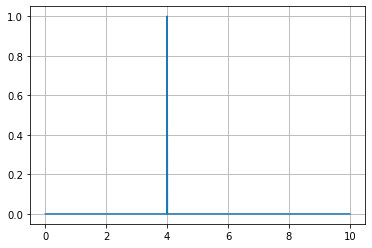
Funciones de Membresía Típicas
Con Derivadas Discontinuas: la derivada sufre cambios abruptos
Triangular
f(x; a, b, c) = \left\{
\begin{matrix}
0 & x \leq a \\
\frac{x-a}{b-a} & a \leq x \leq b \\
\frac{c-x}{c-b} & b \leq x \leq c \\
0 & x \geq c
\end{matrix}
\right. \\
a \leq b \leq c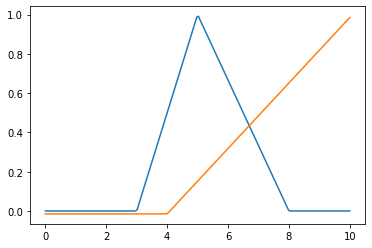
Trapezoidal
f(x; a, b, c, d) = \left\{
\begin{matrix}
0 & x \leq a \\
\frac{x-a}{b-a} & a \leq x \leq b \\
1 & b \leq x \leq c \\
\frac{d-x}{d-c} & c \leq x \leq d \\
0 & x \geq d
\end{matrix}
\right. \\
a \leq b \leq c \leq d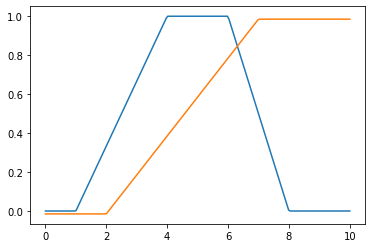
Con derivadas continuas y que son cerradas-simétricas
Gaussiana
f(x; \sigma, x_0) = e^{- \frac{1}{2} \left( \frac{x - x_0}{\sigma} \right)^2 } \\
\sigma : \text{ desv. std., determina el ancho} \\
x_0 : \text{ media, determina el centro }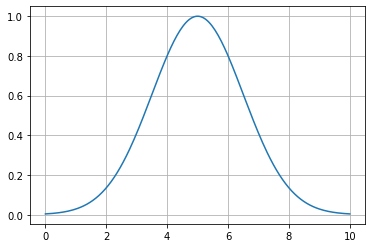
Campana Generalizada
f(x; a, b, x_0) = \frac{1}{ 1 + \left| \frac{x-x_0}{a} \right|^{2b} } \\
a : \text{ determina el ancho } \\
b : \text{ determina la pendiente } \\
x_0 : \text{ fija el centro } \\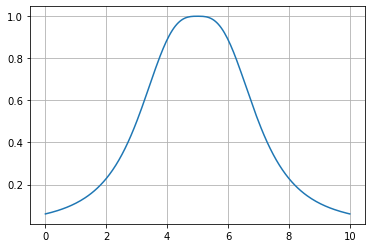
Con derivada continua y abierta
Sigmoidal
f(x; a, x_0) = \frac{1}{ 1 + e^{-a ( x - x_0 )} } \\
a : \text{ determina la pendiente} \\
a > 0 \text{ abre a la derecha} \\
a < 0 \text{ abre a la izquierda} \\
x_0 : \text { determina el punto de cruce } \\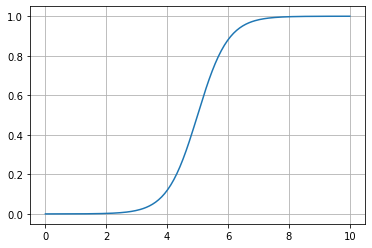
Klir, G. J., & Yuan, B. (1995). Fuzzy Sets and Fuzzy Logic: Theory and Applications. Prentice Hall.
[Hackeando Tec]. (2015, Agosto 21). Lógica Difusa – 1.4 Funciones de Membresía – Parte 1 – Hackeando Tec [Video]. YouTube. https://youtu.be/VexUIkJXzcQ?si=uyOdg0lj9p_RefK0
[Hackeando Tec]. (2015, Agosto 21). Lógica Difusa – 1.4 Funciones de Membresía (Típicas) – Parte 2 – Hackeando Tec [Video]. YouTube. https://youtu.be/gicpjjHYgRY?si=4TphIGPdrbD5kFKw
