Lógica Difusa: Principio de Extensión
Principio de Extensión Unidimensional
\begin{aligned}
f & : X \to Y \\
A & = \left\{ \frac{\mu_A(x_1)}{x_1} + \frac{\mu_A(x_2)}{x_2} + \dots \right\} &
\to B & = \left\{ \frac{\mu_B(y_1)}{y_1} + \frac{\mu_B(y_2)}{y_2} + \dots \right\} \\
\text{donde:} \\
y & = f(x) \\
\mu_B(y) & = \begin{matrix} \huge \lor & \mu_A(x) \\ _{f(x) = y} \end{matrix} = \max_{f(x) = y} \mu_A(x) & & \text{ Caso discreto} \\
\mu_B(y) & = \begin{matrix} \huge \lor & \mu_A(x) \\ _{f(x) = y} \end{matrix} = \sup_{f(x) = y} \mu_A(x) & & \text{ Caso continuo}
\end{aligned}Propiedades del Principio de Extensión
\begin{aligned}
f(A) = \empty & \leftrightarrow A = \empty \\
\text{Si } A_1 \subseteq A_2, & \text{ entonces } f(A_1) \subseteq f(A_2) \\
f(\bigcup_{i \in I} A_i & = \bigcup_{i \in I} f(A_i) \\
f(\bigcap_{i \in I} A_i & \subseteq \bigcap_{i \in I} f(A_i) \\
\text{Si } B_1 \subseteq B_2, & \text{ entonces } f^{-1}(B_1) \subseteq f^{-1}(B_2)
\end{aligned}\begin{aligned}
f^{-1}(\bigcup_{i \in I} B_i) & = \bigcup_{i \in I} f^{-1}(B_i) \\
f^{-1}(\bigcap_{i \in I} B_i) & = \bigcap_{i \in I} f^{-1}(B_i) \\
\overline{f^{-1}(B)} & = f^{-1}(\overline{B}) \\
A & \subseteq f^{-1}(f(A)) \\
B & \supseteq f(f^{-1}(B))
\end{aligned}\begin{aligned}
{}^{\alpha +} [ f(A) ] & = f({}^{\alpha +}A) \\
{}^{\alpha} [ f(A) ] & \supseteq f({}^{\alpha}A) \\
\end{aligned}\begin{aligned}
f(A) & = \bigcup_{\alpha \in [0, 1]} f({}_{\alpha +} A)
\end{aligned}Ejemplo
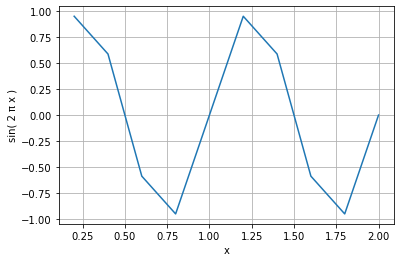
Calcular los conjuntos difusos imagen de f(x) = sen 2πx
\begin{aligned}
A & = \left\{ \frac{0}{0.2} + \frac{0.2}{0.4} + \frac{0.3}{0.6} + \frac{0.4}{0.8} + \frac{0.5}{1.0} + \frac{0.6}{1.2} +\frac{0.7}{1.4} + \frac{0.8}{1.6} + \frac{0.9}{1.8} + \frac{1.0}{2.0} \right\} \\
& \begin{matrix}
x & \to & 0.2 & 0.4 & 0.6 & 0.8 & 1.0 & 1.2 & 1.4 & 1.6 & 1.8 & 2.0 \\
f(x) & \to & 0.951 & 0.588 & -0.588 & -0.951 & -0.0 & 0.951 & 0.588 & -0.588 & -0.951 & -0.0
\end{matrix} \\
\therefore \\
B & = \left\{ \frac{ \max( 0.4, 0.9 ) }{ -0.951 } + \frac{ \max( 0.3, 0.8 ) }{ -0.588 } + \frac{ \max( 0.5, 1.0 ) }{ -0.0 } + \frac{ \max( 0.2, 0.7 ) }{ 0.588 } + \frac{ \max( 0.0, 0.6 ) }{ 0.951 } \right\} \\
& = \left\{ \frac{ 0.9 }{ -0.951 } + \frac{ 0.8 }{ -0.588 } + \frac{ 1.0 }{ -0.0 } + \frac{ 0.7 }{ 0.588 } + \frac{ 0.6 }{ 0.951 } \right\}
\end{aligned}Principio de Extensión Multidimensional
\begin{aligned}
f & : (X_1 \times X_2 \times \cdots \times X_n) \to Y \\
& A_1, A_2, \dots , A_n \text{ definidos en } X_1, X_2, \dots , X_n \\
& \Rightarrow \\
B & = f( A_1, A_2, \dots , A_n ) \\
& \text{ donde } y = f( x_1, \dots , x_n ) \\
\mu_B & = \begin{matrix} \huge \lor & [\mu_{A_1}(x_1) \land \mu_{A_2}(x_2) \land \cdots \land \mu_{A_n}(x_n)] \\ f( x_1, \dots , x_n ) = y \end{matrix} \\
& = \max_{f( x_1, \dots , x_n )} \left\{ \min [ \mu_{A_1}(x_1) , \dots , \mu_{A_n}(x_n) ] \right\} & \text{ Caso discreto} \\
& = \sup_{f( x_1, \dots , x_n )} \left\{ \inf [ \mu_{A_1}(x_1) , \dots , \mu_{A_n}(x_n) ] \right\} & \text{ Caso continuo}
\end{aligned}Calcular los conjuntos difusos imagen de f(x1, x2) = x12 + x22 evaluándo en los siguientes conjuntos difusos:
\begin{aligned}
A_1 & = \left\{ \frac{1}{-2} + \frac{0.9}{-1} + \frac{0.5}{0} + \frac{0.1}{1} + \frac{0}{2} \right\} &
A_2 & = \left\{ \frac{0}{-2} + \frac{0.5}{-1} + \frac{1}{0} + \frac{0.5}{1} + \frac{0}{2} \right\} \\
\end{aligned}\begin{aligned}
B = f( A_1, A_2 )
& = \begin{matrix}
\huge \lor
& \begin{matrix}
\begin{matrix} -2 \\ -1 \\ 0 \\ 1 \\ 2 \end{matrix} &
\begin{bmatrix}
^{ \min (1, 0) }/_{( -2 )^2 + ( -2 )^2} & ^{ \min (1, 0.5) }/_{( -2 )^2 + ( -1 )^2} & ^{ \min (1, 1) }/_{( -2 )^2 + ( 0 )^2} & ^{ \min (1, 0.5) }/_{( -2 )^2 + ( 1 )^2} & ^{ \min (1, 0) }/_{( -2 )^2 + ( 2 )^2} \\
^{ \min (0.9, 0) }/_{( -1 )^2 + ( -2 )^2} & ^{ \min (0.9, 0.5) }/_{( -1 )^2 + ( -1 )^2} & ^{ \min (0.9, 1) }/_{( -1 )^2 + ( 0 )^2} & ^{ \min (0.9, 0.5) }/_{( -1 )^2 + ( 1 )^2} & ^{ \min (0.9, 0) }/_{( -1 )^2 + ( 2 )^2} \\
^{ \min (0.5, 0) }/_{( 0 )^2 + ( -2 )^2} & ^{ \min (0.5, 0.5) }/_{( 0 )^2 + ( -1 )^2} & ^{ \min (0.5, 1) }/_{( 0 )^2 + ( 0 )^2} & ^{ \min (0.5, 0.5) }/_{( 0 )^2 + ( 1 )^2} & ^{ \min (0.5, 0) }/_{( 0 )^2 + ( 2 )^2} \\
^{ \min (0.1, 0) }/_{( 1 )^2 + ( -2 )^2} & ^{ \min (0.1, 0.5) }/_{( 1 )^2 + ( -1 )^2} & ^{ \min (0.1, 1) }/_{( 1 )^2 + ( 0 )^2} & ^{ \min (0.1, 0.5) }/_{( 1 )^2 + ( 1 )^2} & ^{ \min (0.1, 0) }/_{( 1 )^2 + ( 2 )^2} \\
^{ \min (0, 0) }/_{( 2 )^2 + ( -2 )^2} & ^{ \min (0, 0.5) }/_{( 2 )^2 + ( -1 )^2} & ^{ \min (0, 1) }/_{( 2 )^2 + ( 0 )^2} & ^{ \min (0, 0.5) }/_{( 2 )^2 + ( 1 )^2} & ^{ \min (0, 0) }/_{( 2 )^2 + ( 2 )^2}
\end{bmatrix} \\
& \begin{matrix} -2 & & & & & & & & & -1 & & & & & & & & & 0 & & & & & & & & & 1 & & & & & & & & & 2 \end{matrix}
\end{matrix} \\
_{f(x_1, x_2)}
\end{matrix} \\
& = \begin{matrix}
\huge \lor
& = \begin{matrix}
\begin{matrix} -2 \\ -1 \\ 0 \\ 1 \\ 2 \end{matrix} &
\begin{bmatrix}
^{ 0 }/_{ 8 } & ^{ 0.5 }/_{ 5 } & ^{ 1 }/_{ 4 } & ^{ 0.5 }/_{ 5 } & ^{ 0 }/_{ 8 } \\
^{ 0 }/_{ 5 } & ^{ 0.5 }/_{ 2 } & ^{ 0.9 }/_{ 1 } & ^{ 0.5 }/_{ 2 } & ^{ 0 }/_{ 5 } \\
^{ 0 }/_{ 4 } & ^{ 0.5 }/_{ 1 } & ^{ 0.5 }/_{ 0 } & ^{ 0.5 }/_{ 1 } & ^{ 0 }/_{ 4 } \\
^{ 0 }/_{ 5 } & ^{ 0.1 }/_{ 2 } & ^{ 0.1 }/_{ 1 } & ^{ 0.1 }/_{ 2 } & ^{ 0 }/_{ 5 } \\
^{ 0 }/_{ 8 } & ^{ 0 }/_{ 5 } & ^{ 0 }/_{ 4 } & ^{ 0 }/_{ 5 } & ^{ 0 }/_{ 8 }
\end{bmatrix} \\
& \begin{matrix} -2 & & -1 & & 0 & & 1 & & 2 \end{matrix}
\end{matrix} \\
_{f(x_1, x_2)}
\end{matrix} \\
& = \left\{ \frac{ \max ( 0.5 )}{ 0 } + \frac{ \max ( 0.9, 0.5, 0.5, 0.1 )}{ 1 } + \frac{ \max ( 0.5, 0.5, 0.1, 0.1 )}{ 2 } + \frac{ \max ( 1, 0, 0, 0 )}{ 4 } + \frac{ \max ( 0.5, 0.5, 0, 0, 0, 0, 0, 0 )}{ 5 } + \frac{ \max ( 0, 0, 0, 0 )}{ 8 } \right\} \\
& = \left\{ \frac{ 0.5 }{ 0 } + \frac{ 0.9 }{ 1 } + \frac{ 0.5 }{ 2 } + \frac{ 1 }{ 4 } + \frac{ 0.5 }{ 5.0 } + \frac{ 0 }{ 8 } \right\}
\end{aligned}Klir, G. J., & Yuan, B. (1995). Fuzzy Sets and Fuzzy Logic: Theory and Applications. Prentice Hall.
[Hackeando Tec]. (2015, Agosto 23). Lógica Difusa – 2.3.1 Principio de Extensión Unidimensional – Hackeando Tec [Video]. YouTube. https://youtu.be/iL010yhQFLU?si=aoCuC763Xj8EBNqR
[Hackeando Tec]. (2015, Agosto 23). Lógica Difusa – 2.3.2 Principio de Extensión Multidimensional – Hackeando Tec [Video]. YouTube. https://youtu.be/IMslXhHvTFA?si=BdiQDhPG_49mWoiy
